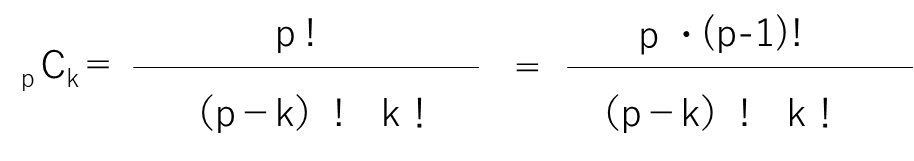フェルマーの小定理は、次のものです。
pが素数で、aがpの倍数でない正の整数のとき、
ap-1≡1(mod p)
です。
少し説明しますと、仮に、p=5、a=1, 2, 3, 4,6, 7のとき、ap-1は、次の値を取ります。
14=1
24=16
34=81
44=256
64=1256
74=2401
これらの値を5で割ると、あまりがすべて1です。つまりa4≡1 (mod 5)が成立しています。
今回の証明その1は、数学的帰納法を用います。
つまり、任意の正の整数aに対して、ap≡aであることを示せば、以前説明した(2021年11月18日の本ブログ参照)定理「aとpが互いに素なときは、合同式の両辺をaで割ることができる」を使うことにより、上式の両辺をaで割れば、フェルマーの小定理が求まります。
さて、a=1のとき、あきらかにaP≡aです。
二項定理を使うこととします。
2項定理の
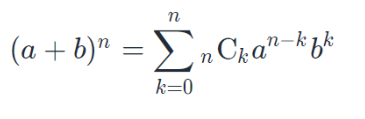
から、a→1、b→mとおくと、
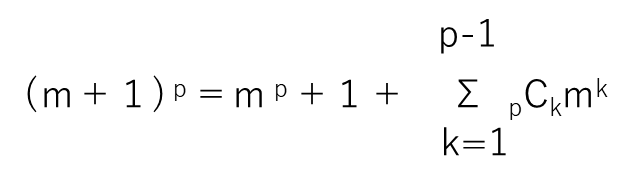
となり、pが素数で、1≦k≦p-1のとき、pCkがpの倍数であるから(※)
mp≡mなら、(m+1)p≡m+1が成立する。
以上から、数学的帰納法から、すべてのaに対してap≡a であり、証明されたことになります。
※これは2項係数の一つの性質であります。