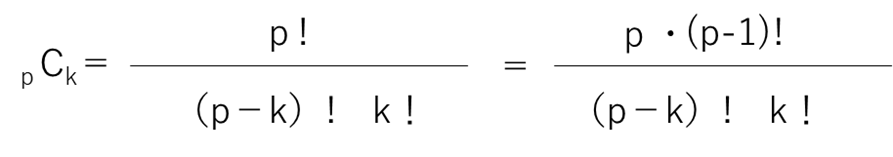フェルマーの小定理の証明その２

　以前に述べたとおり、フェルマーの小定理は、次のとおりです。

pが素数で、aがpの倍数でない正の整数のとき、

　　a^p-1≡1（mod ｐ）

です。

今回は、このフェルマーの小定理の証明その２です。

　まず、2項定理から

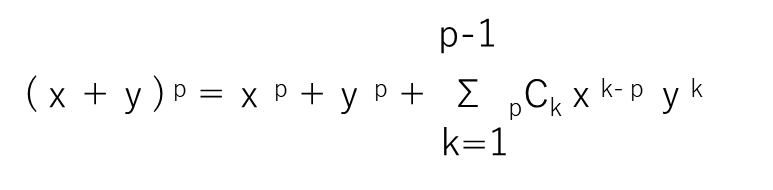
となり、pが素数で、１≦k≦p－1のとき、_pC_kがpの倍数であるから（※）

(ｘ＋ｙ)^ｐ≡ｘ^ｐ＋ｙ^ｐ（mod p）

これより、

a^p=〔１+(a-1)〕^p
≡1^p+〔１+(a-2)〕^p
≡１＋1^p+〔１+(a-３)〕^p
≡２＋1p+〔１+(a-4)〕^p
≡ ・・・・
≡a-2＋1^p+〔１+(a-a)〕^p
≡a　(mod p)

ここで、aとｐとは、たがいに素であるので、両辺をaで割ることができ、a^p-1≡1（mod ｐ）が証明されました。

※これは、前も出てきました2項係数の一つの性質であります。