算数・数学コラム

虚数の問題は極形式で解く

2023年2月6日

虚数の方程式を解く問題が鈴木貫太郎先生のYouTubeに出ていました。

長崎大（医、他）虚数方程式
https://www.youtube.com/watch?v=1f7N5kIIVv8

こういった問題は、極形式で考えるのですよね。ということで、以下答案です。

解けそうにない問題がいつの間にか解けるようになるのは、子供も大人もウレシイですね。

雑記

i（虚数）をｉ乗すると実数、それも複数の実数になるって(’ω’)

2020年11月8日

ｉを二乗すると-1になるというのは、昔習いましたが、そのｉをｉ乗するとどうなるかなんてことを、気にしたことはありませんでしたか？

実は、その答えの一つは以前の当Blog（2020年8月18日）で紹介したオイラーの公式

$e^{i\theta }=\cos \theta +i\sin \theta$

を使うと求められます。

iⁱ＝exp(logiⁱ)

=exp(i＊log(i))

=exp(i＊(log|i|+i＊arg(i)))

=exp(0-arg(i))

=exp(-(2n+1/2）＊π）　n=0,±1,±2, …

ここで、n=0のとき　exp(-π/2)＝0.20787957635…となります。n＝+１のとき、exp(-5/2π)＝0.00038820320…となります。

つまり、答えは、iⁱ=…,e^−9π/2, e^−5π/2, e^−π/2, e^3π/2, e^7π/2, …　と、実数が、一杯出てくるようです。　驚きですよね～！！

参考文献は、次の通りです:

https://ja.wikipedia.org/wiki/I%E3%81%AEi%E4%B9%97

https://tsujimotter.hatenablog.com/entry/i-to-the-power-of-i

算数・数学コラム

えええ、昔の東大入試って？

2023年7月20日

こんな問題が出ていたようです。

1926東京帝国大学　虚数単位 i の立方根を求める【数検1級/準1級/大学数学/高校数学/数学教育】　
https://www.youtube.com/watch?v=WDNDGjeZpTo

以下解答です。

これなら、私も東大生？

算数・数学コラム

2次方程式の根と係数の関係は複素数の場合でも成立するのだ(^_-)-☆

2023年3月20日

今年の慶応大学医学部の入試問題を鈴木貫太郎先生も取り上げていました。

慶應（医）虚数係数の二次方程式の２解の距離
https://www.youtube.com/watch?v=iGZAso0DYak

これを、3通りの方法で解きました。以下、解答です。

まあ、どうやっても解けるんですけどね、エレガントにいきたいですね。(^_-)-☆

算数・数学コラム

連立2元4次方程式は解けるか？

2022年10月26日

またしても、鈴木貫太郎先生の問題です。

連立２元４次方程式
https://www.youtube.com/watch?v=sRi9UYVdj9o

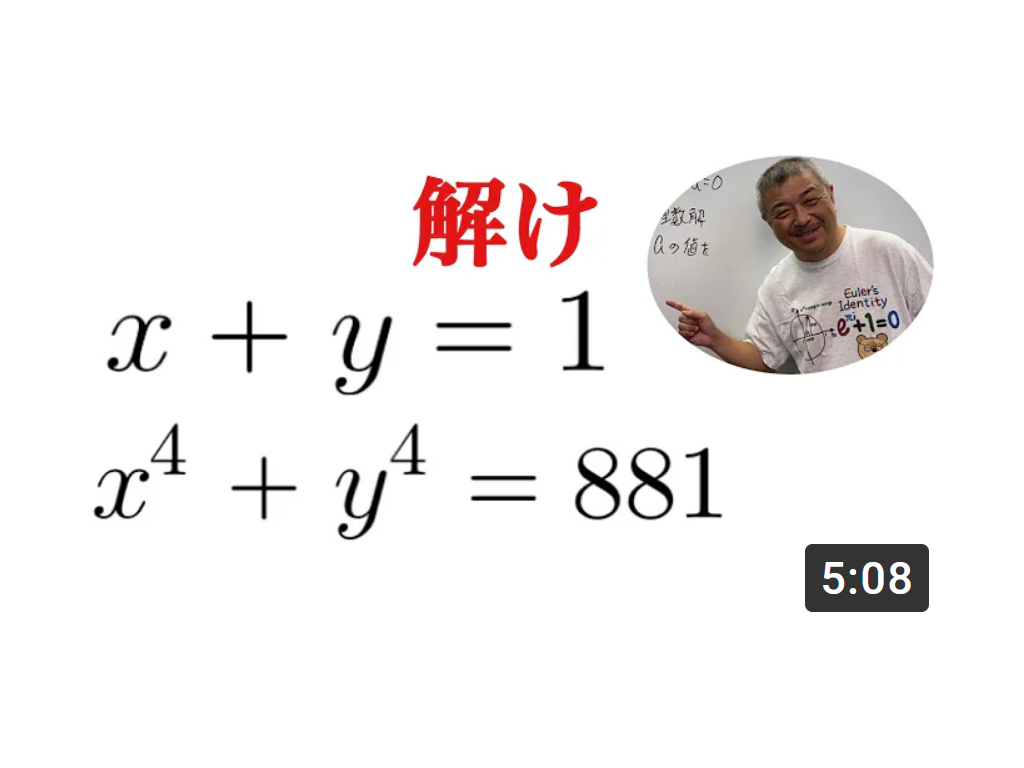
解いてみました。以下、私の答案です。

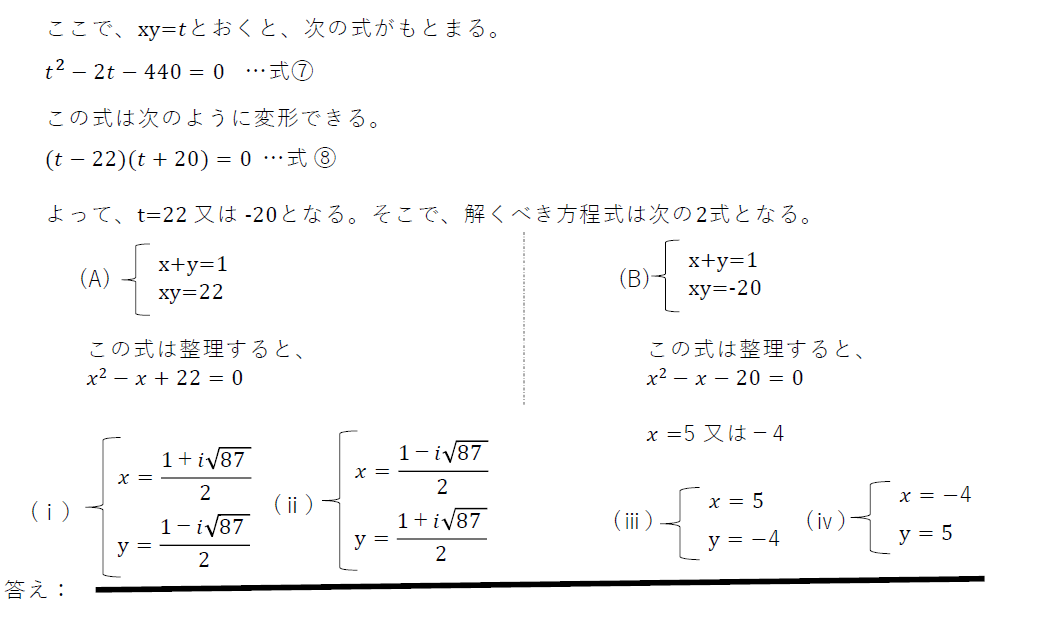
解けた！　解けた！　ということで、以前もｘ＋ｙとｘｙの式になったものがあったような。
4次方程式なので、4つ解があり、2つは実数解、2つは虚数解になってますね。

雑記

あなたはトリボナッチ数列とかテトラナッチ数列とか知ってますか？

2020年12月28日

先にフィボナッチ数列の紹介をしました(2020年8月26日)。このとき、自然数の数列なのに、その一般項を求めると、無理数の差で表されていたということが驚きでした。

トリボナッチ数列は、同様に、次の自然数の数列で、前3つの数字を足した数列（0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768,…）です。

この一般項には、今度は虚数（i）が含まれるというので驚きです。Wikipedia　（https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A3%E3%83%9C%E3%83%8A%E3%83%83%E3%83%81%E6%95%B0#%E3%83%88%E3%83%AA%E3%83%9C%E3%83%8A%E3%83%83%E3%83%81%E6%95%B0）によれば、その一般項は次のように記すことができるようです。

{\displaystyle T_{n}={\frac {\alpha ^{n}}{(\alpha -\beta )(\alpha -\gamma )}}+{\frac {\beta ^{n}}{(\beta -\gamma )(\beta -\alpha )}}+{\frac {\gamma ^{n}}{(\gamma -\alpha )(\gamma -\beta )}}}

ただし、α, β, γ は三次方程式 x³ − x² − x − 1 = 0 の3つの解

{\displaystyle {\begin{aligned}\alpha &={\frac {1}{3}}\left(1+{\sqrt[{3}]{19-3{\sqrt {33}}}}+{\sqrt[{3}]{19+3{\sqrt {33}}}}\right)\\\beta &={\frac {1}{3}}\left(1+\omega {\sqrt[{3}]{19-3{\sqrt {33}}}}+{\bar {\omega }}{\sqrt[{3}]{19+3{\sqrt {33}}}}\right)\\\gamma &={\frac {1}{3}}\left(1+{\bar {\omega }}{\sqrt[{3}]{19-3{\sqrt {33}}}}+\omega {\sqrt[{3}]{19+3{\sqrt {33}}}}\right)\end{aligned}}}

であり、ここでｗは、1の虚立方根、

{\displaystyle \omega ={\frac {-1+{\sqrt {3}}i}{2}}}

です。なお、α をトリボナッチ定数といい、隣接2項間の商はトリボナッチ定数に収束するということです。

{\displaystyle \lim _{n\to \infty }{\frac {T_{n}}{T_{n-1}}}=\alpha =1.839286755214161\cdots }

同様に、前４つの数字を足した値となる数列（0, 0, 0, 1, 1, 2, 4, 8, 15, 29, 56, 108, 208, 401, 773, 1490, 2872, 5536,…）がテトラナッチ数列です。その一般項は、四次方程式 x⁴ − x³ − x² − x − 1 = 0 の4つ解を α, β, γ, δ として、

{\displaystyle T_{n}={\frac {\alpha ^{n}}{(\alpha -\beta )(\alpha -\gamma )(\alpha -\delta )}}+{\frac {\beta ^{n}}{(\beta -\gamma )(\beta -\delta )(\beta -\alpha )}}+{\frac {\gamma ^{n}}{(\gamma -\delta )(\gamma -\alpha )(\gamma -\beta )}}+{\frac {\delta ^{n}}{(\delta -\alpha )(\delta -\beta )(\delta -\gamma )}}}

となるとのこと。

今回のこのトリボナッチ数列のことも、ヨビノリのたくみ先生のYouTube講義「中学数学からはじめる複素数」https://www.youtube.com/watch?v=IQaYyFboK48　で知りました　!(^^)!