数学検定１級１次計算技能検定問題２

第２問です。複素数の三角関数ということで、あらら？と戸惑ってしまいますが、ある公式を思い出せば、なんのことはない問題です。

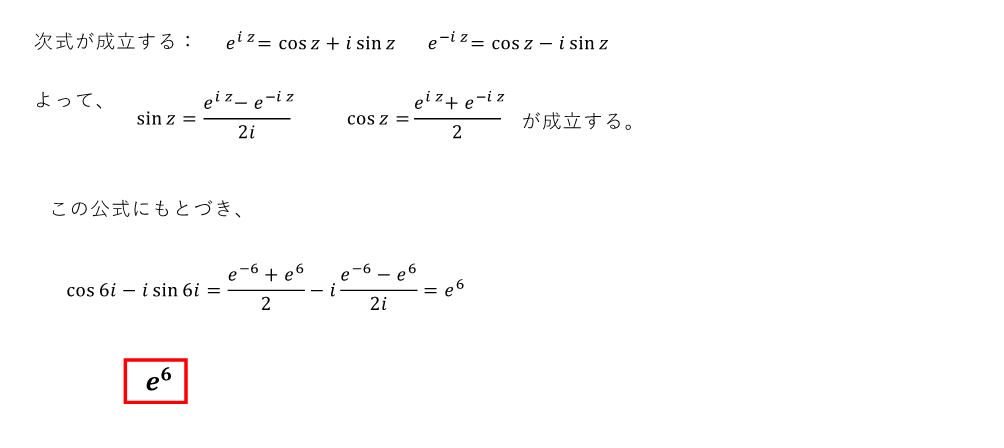
数学も、このような記憶が必要になるのですね。知っているとすぐ解けますが、知らないと手も足も出ないものです。しかし、虚数を含む三角関数の計算を行った結果、実数の解が出るというのは、摩訶不思議に思う次第です。実と虚の間は（e）exponential　で繋がっているのですね。

「オイラーの公式　e^(iθ) = cosθ + isinθ　の美しさは、異なる概念（指数関数、三角関数、虚数）が1つの等式で表現されている点にあります。この公式は、数学の奥深さと美しさを象徴する存在として、多くの人々に愛されています。」と言われる所以です。